Prediction Theory for Gaussian Process Regression

摘要

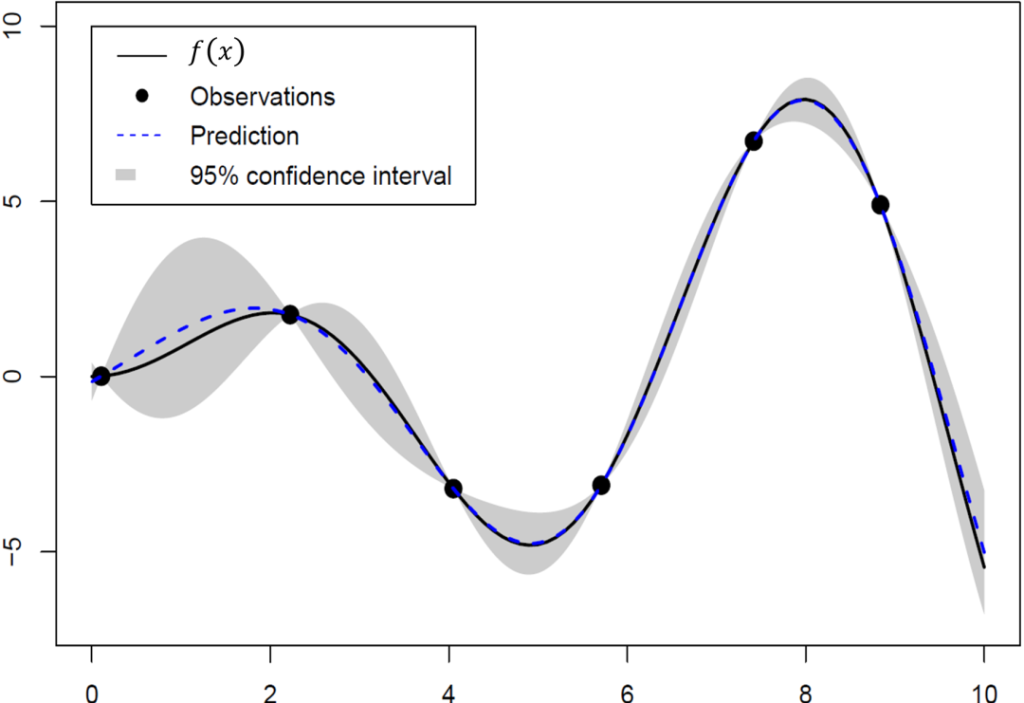
Gaussian process regression is widely used in many fields, for example, machine learning, reinforcement learning and uncertainty quantification. The goal of Gaussian process regression is to recover an underlying function based on noisy observations. As a Bayesian machine learning method, the key idea of Gaussian process regression is to impose a probabilistic structure, which is a Gaussian process, on the underlying truth. Based on this assumption, the conditional distribution at each unobserved point in the interested domain is normal with explicit mean and variance. The conditional mean provides a natural predictor of the function value, and the pointwise confidence interval constructed based on the conditional variance can be used for statistical uncertainty quantification.

In a series of works, we derive non-asymptotic lower and upper error bounds of the (simple) kriging predictor under a uniform metric and Lp metric. The kriging predictor can be mis-specified, and the observations can have noise. In particular, we show that if the design is quasi-uniform and an oversmoothed correlation function is used, the upper bound and lower bound coincide, up to a constant multiplier. The optimal rate has been achieved in this scenario. As an application of our results, we apply our theory to machine learning. Although Bayesian optimization is widely used in areas including deep neural networks and reinforcement learning, uncertainty quantification of the outputs is rarely studied in the literature. We propose a novel approach to assess the output uncertainty of Bayesian optimization. To the best of our knowledge, this is the first result of this kind. Our theory also provides a unified uncertainty quantification framework for all existing sequential sampling policies and stopping criteria.