Improving Generalization in Equivariant Graph Neural Networks with Physical Inductive Biases

Abstract

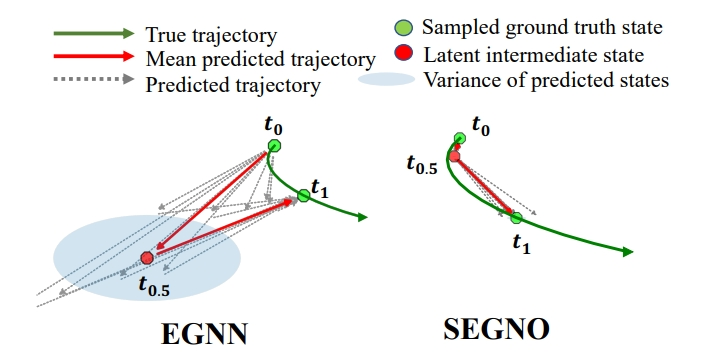
Graph Neural Networks (GNNs) with equivariant properties have emerged as powerful tools for modeling complex dynamics of multi-object physical systems. However, their generalization ability is limited by the inadequate consideration of physical inductive biases: (1) Existing studies overlook the continuity of transitions among system states, opting to employ several discrete transformation layers to learn the direct mapping between two adjacent states; (2) Most models only account for first-order velocity information, despite the fact that many physical systems are governed by second-order motion laws. To incorporate these inductive biases, we propose the Second-order Equivariant Graph Neural Ordinary Differential Equation (SEGNO). Specifically, we show how the second-order continuity can be incorporated into GNNs while maintaining the equivariant property. Furthermore, we offer theoretical insights into SEGNO, highlighting that it can learn a unique trajectory between adjacent states, which is crucial for model generalization. Additionally, we prove that the discrepancy between this learned trajectory of SEGNO and the true trajectory is bounded. Extensive experiments on complex dynamical systems including molecular dynamics and motion capture demonstrate that our model yields a significant improvement over the state-of-the-art baselines.